Bit hacks are an incredibly powerful tool in every developer's toolbox. When used correctly, they can bring simplicity, performance, scalability, and even be used for compact data representation in probabilistic Data Structures.
The downside is that they are hard to understand, need a lot of testing, and in a lot of cases, they aren't portable since these operations will have different outcomes on different hardware architectures.
Don't worry. I'm here to help.
In this article, we will be discussing the usage of bit hacks in the following scenarios:
- Bit Hacks Basics.
- Bit Hacks for Simplicity.
- Bit Hacks for Branch Elimination.
There are many more interesting use cases, but we have to start somewhere. This is the first article in a series of articles about bit manipulations, performance, CPUs, software, and unicorns.
Bit Hacks Basics:
Let's start with a couple of straightforward examples that will be int32 numbers.

Each number can be represented by a set of bytes that are composed of (usually) 8 bits. Having this kind of representation is already useful since we can encode information on its surface.
Let's look at how to set a bit at a given index:
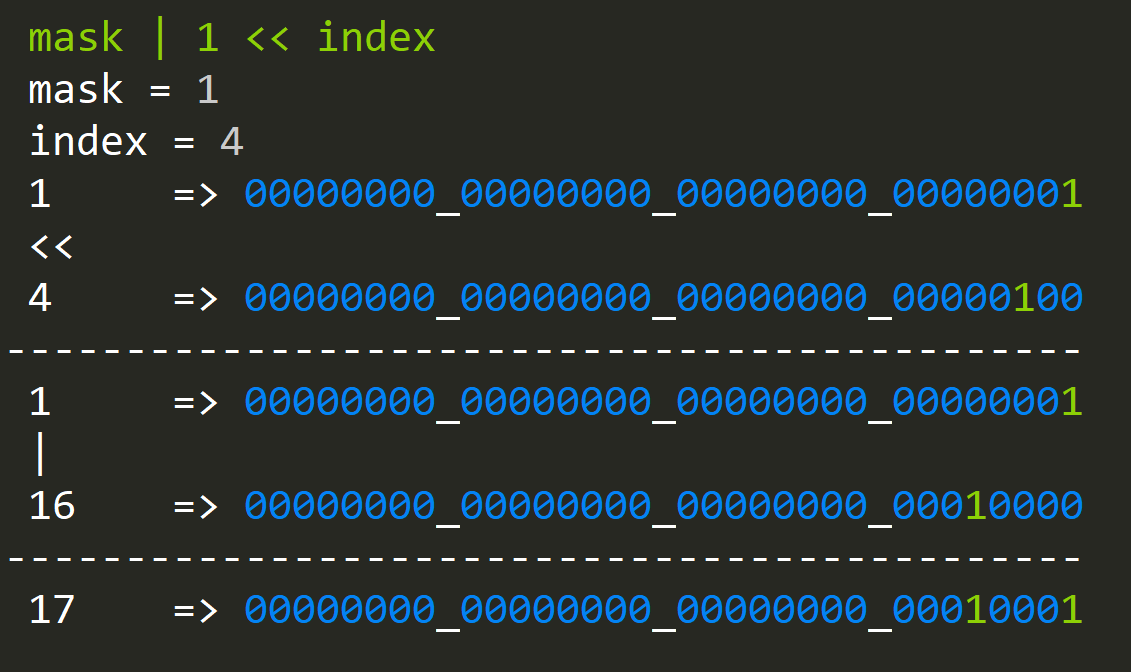
What's going on here?
- We shift our single bit at position 0 to the index position now; we have a single bit in that position.
- We OR it with our existing value mask (1), and since OR will merge all of the ones from two numbers, we now have a bit set at the desired index.
Now that we know how to set bits, we would also like to know if a bit is set at a specified index:
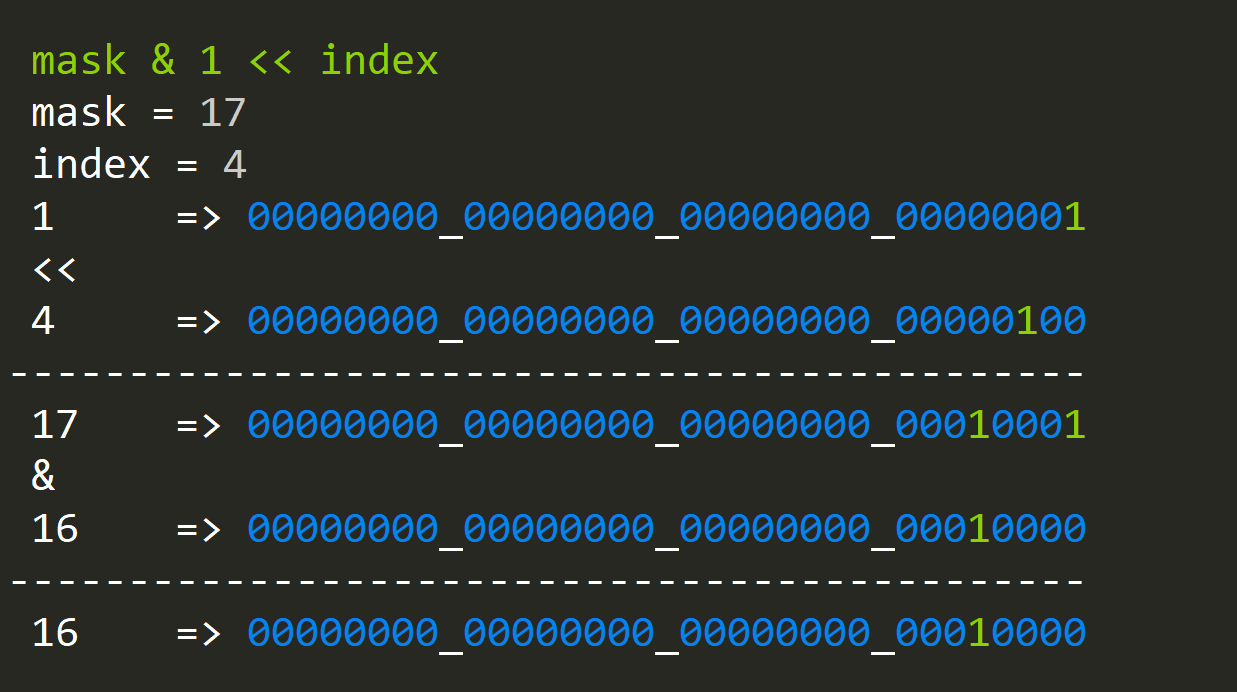
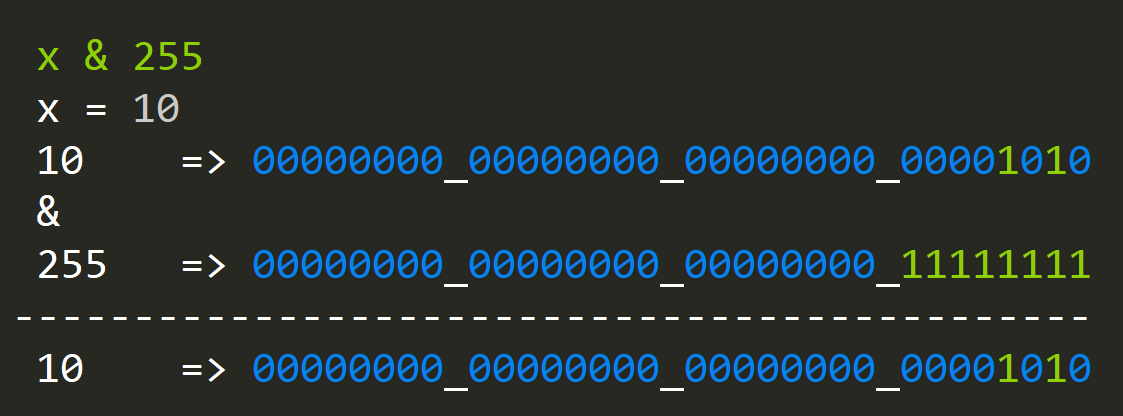
Again the procedure is the same, but instead of OR(ing), we are AND(ing), since if our index is indeed set, the value will be greater then zero.
If we wanted to have a result boolean result; 1 for true; 0 for false we could take out a single status bit and shift it back by the same index as before:
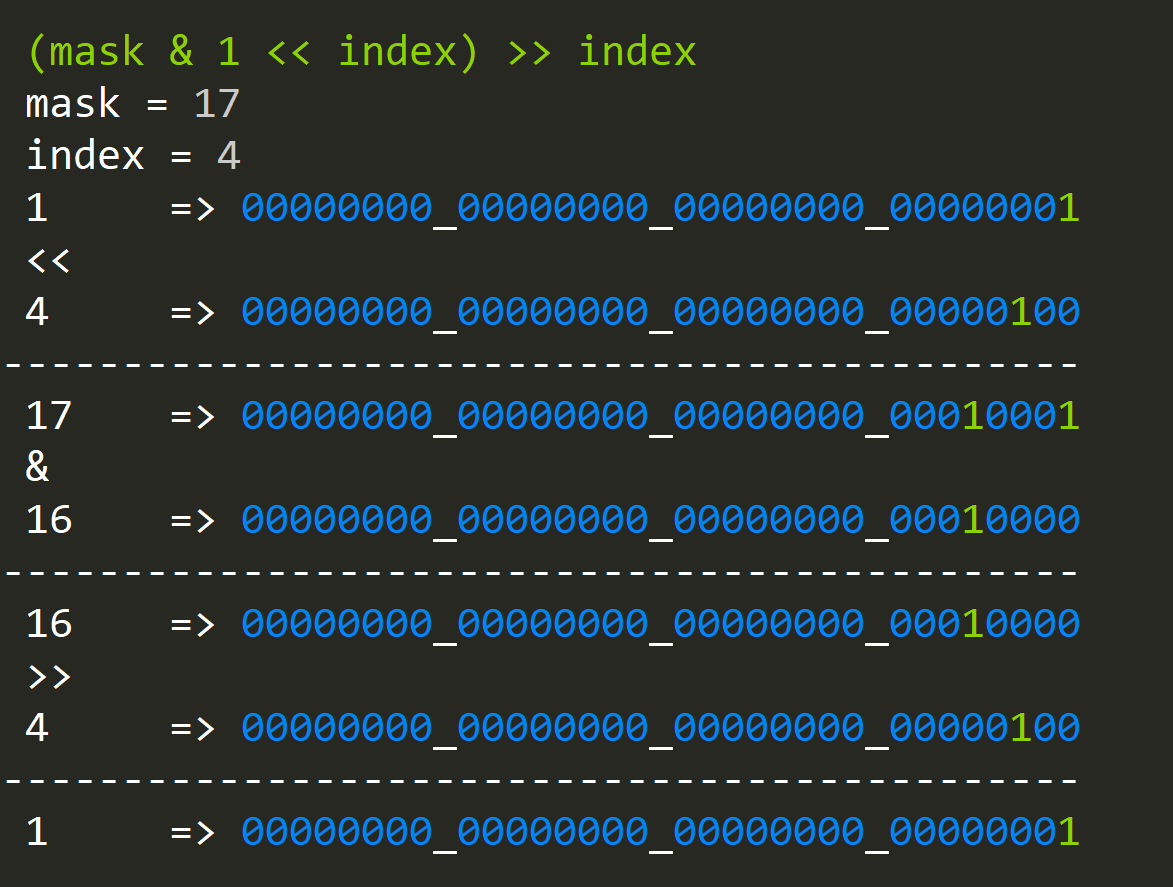
Bit Hacks for Simplicity:
And with only two simple bit expressions, we have implemented a Data Structure called a BitSet.
public class BitSet
{
private int[] bitset;
public BitSet(int size)
{
bitset = new int[size / 32];
}
public void Add(int index)
{
bitset[index / 32] |= (1 << (index % 32));
}
public bool Contains(int index)
{
return (bitset[index / 32] & (1 << (index % 32))) != 0;
}
}
This data structure can be used (amongst hundreds of other things) to have a compact representation of big sets, let me give you an example:
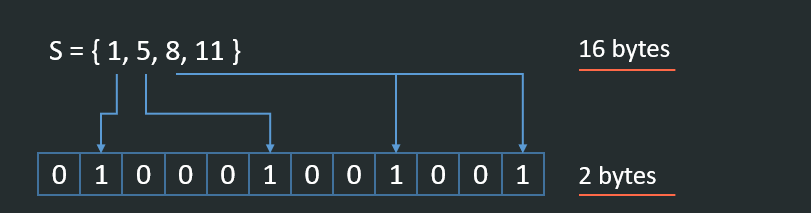
Given a set:
S = { 1, 5, 8, 11 }
How do we check if value: 8 is present in the set? Usually, we would need to load the set first or keep it in the form of HashSet. Both of these structures have a rather high cost; for example, remember that large data storage systems can easily track a set of billions and trillions of elements.
And so enter BitSets where this representation is rather trivial, and this map uses just a couple of bits. The bit set will be the size of the largest element in the collection (we can fix this as well, but this is out of the scope of this article).
Bit Hacks Basics (2):
Ok, so now that we have that out of the way, it's time to learn some quick and simple recipes on how to construct simple bit hacks for fun, performance, and profit.
- How to zero value?
zero = value ^ value
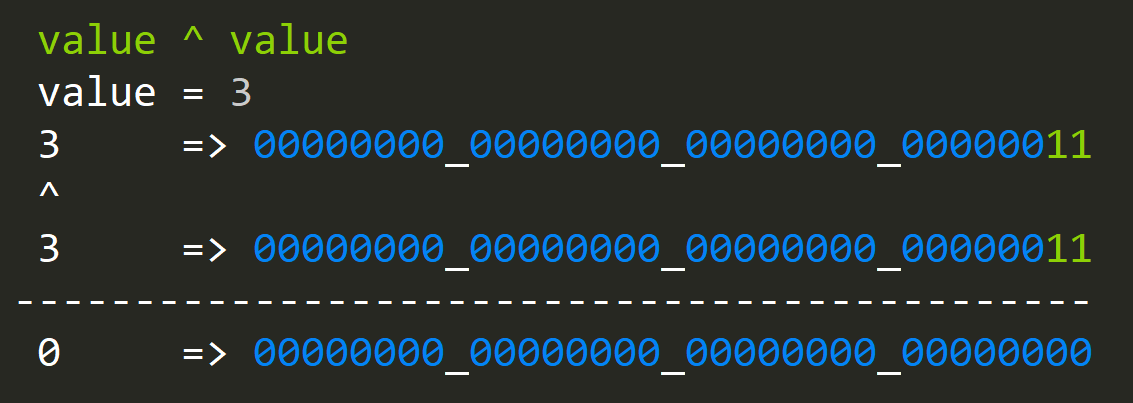
XOR(ing) only sets bits where we have [0;1] or [1;0] in the XOR(ed) values. That's not very useful, but let's build on this simple idea.
You might be wondering why is this even here? We could just assign zero and move on with our lives but let me explain. Like I said before, it's here to get us started, but still, this operation has its uses; when doing SIMD instructions, we don't always have access to zeroing a value; negation intrinsic is only possible on newest CPUs.
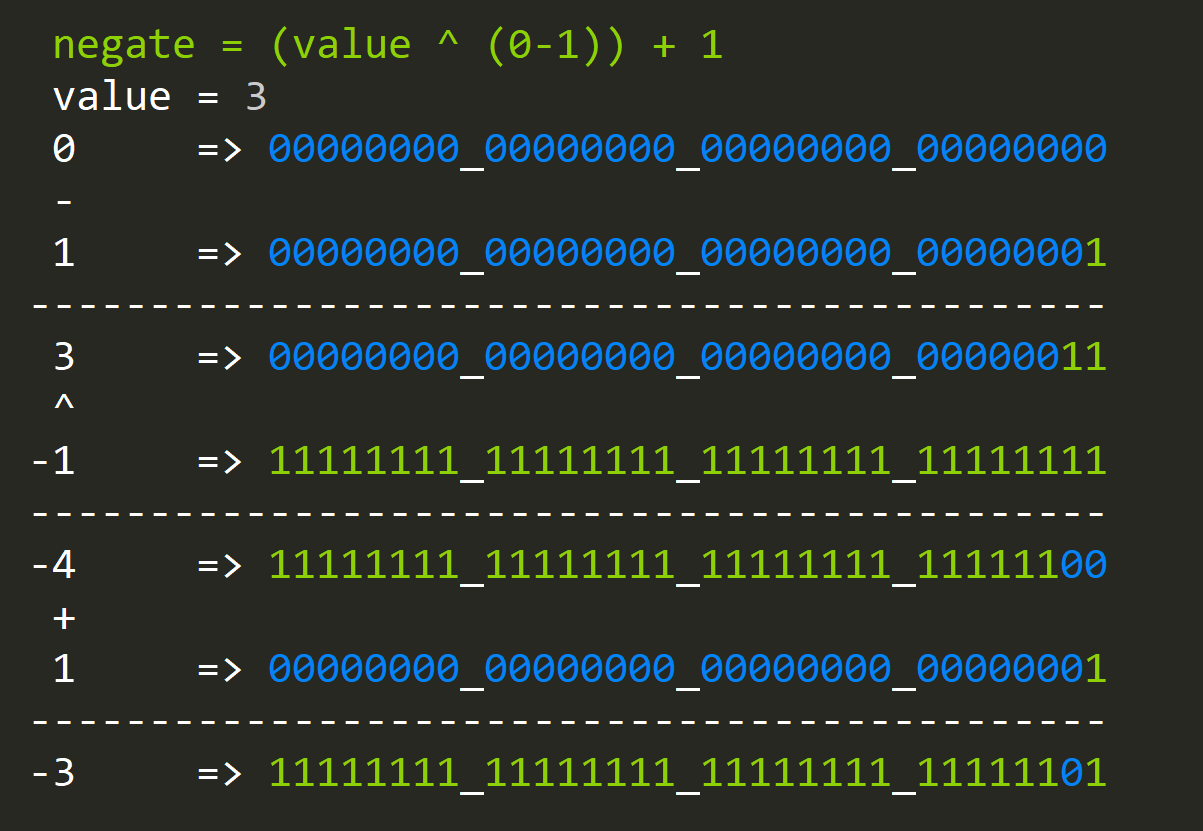
- How to negate a value?
negate = (value ^ -1) + 1
- How to conditionally negate a value?
negate = (flag ^ (flag - 1)) * value
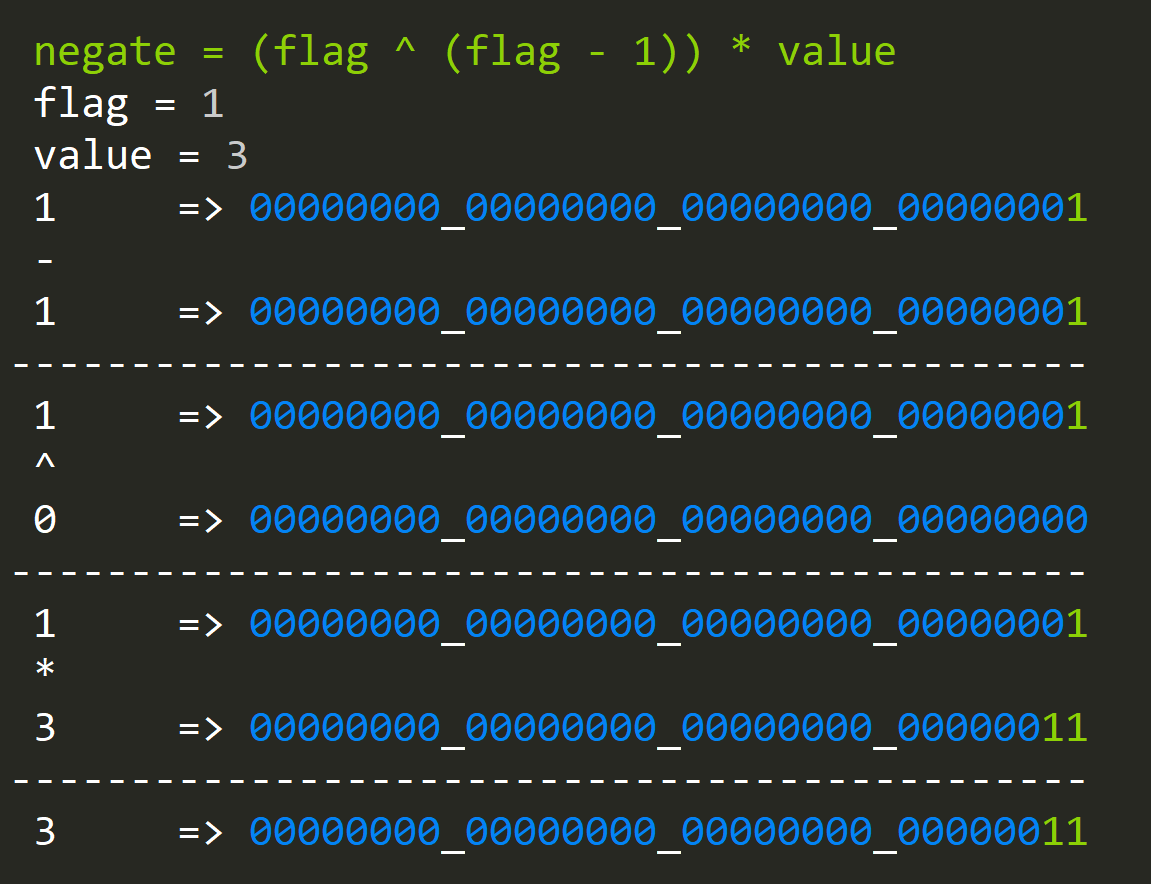
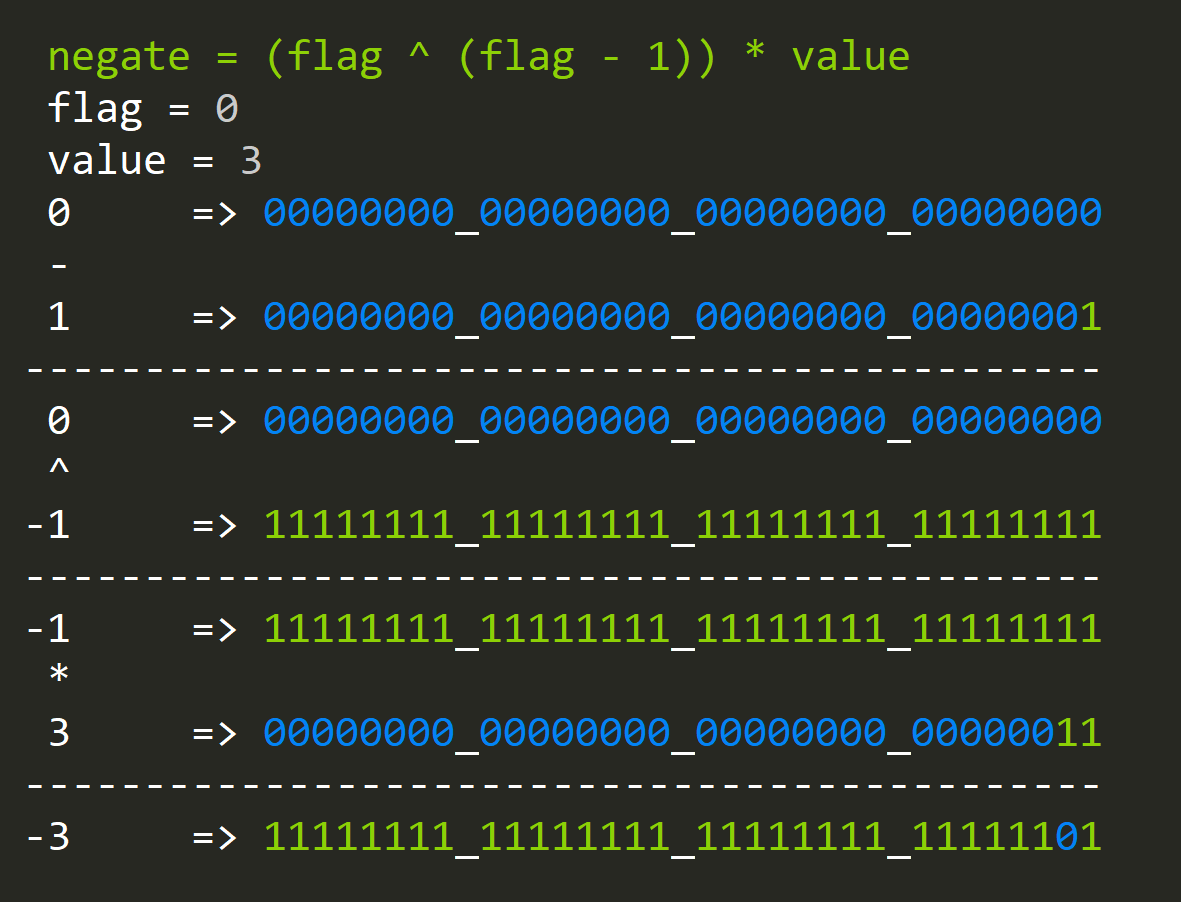
Where the "flag" variable is either 0 (negate) or 1 (leave alone).
The interesting thing about this example is that XOR(ing) an odd number with the same odd number minus one (even) will produce one ... always since odd numbers will always have their first-bit set, and even numbers won't.
But multiplication is not the fastest and besides you can just do:
value * flag
You're right, so let me show you a better version that's a bit harder to replicate without bit hacks.
negate = (value ^ -( flag)) + flag
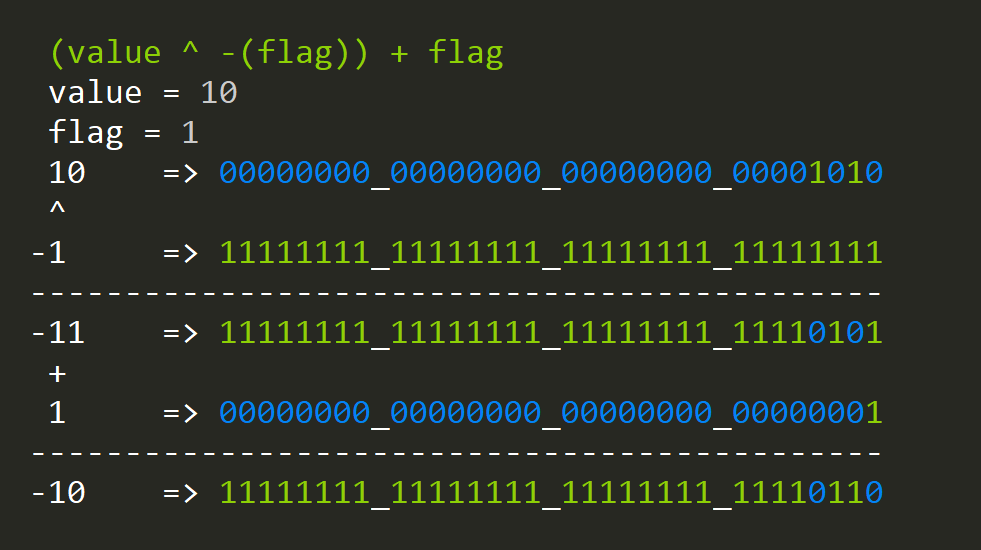
- How to calculate the modulo without using the mod operator?
mod = value & (d - 1)
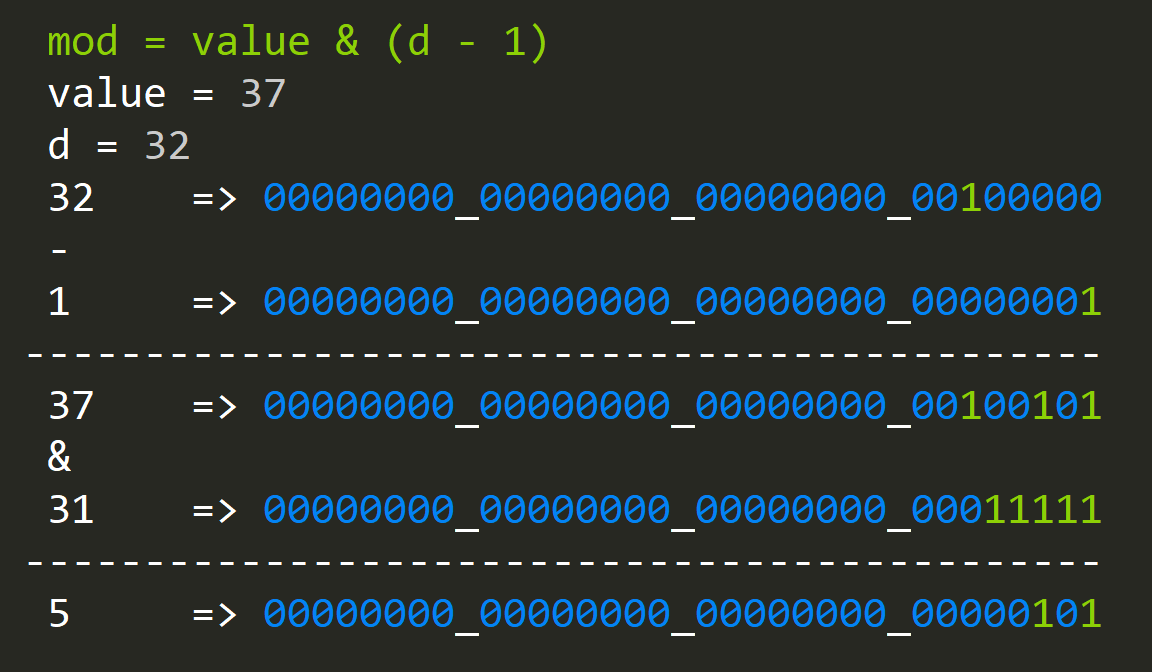
There's a catch here that "d" needs to be the power of two, but there's still a large number of use cases that we can use this.
- How to check the sign of an integer?
sign = value >> (sizeof(int) * 8 - 1)
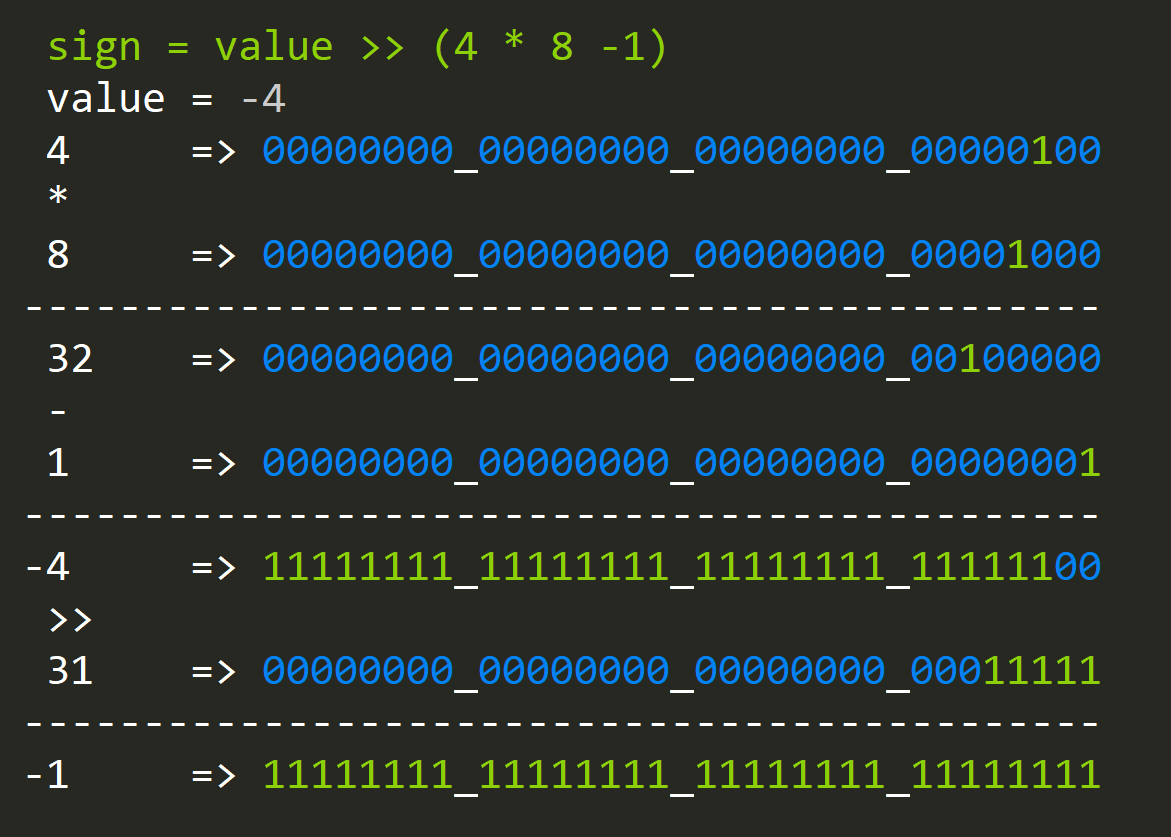
Where the right-hand side is being shifted by can be understood as taking 31 unsigned bits from an Integer. The interesting thing happens when we shit and overflow like that; we copy the sign bit 31 times.
So far so good, using all of the tricks above let's construct a more interesting one:
- How to compute the absolute value of an integer?
abs = value + (value >> 31) ^ (value >> 31)
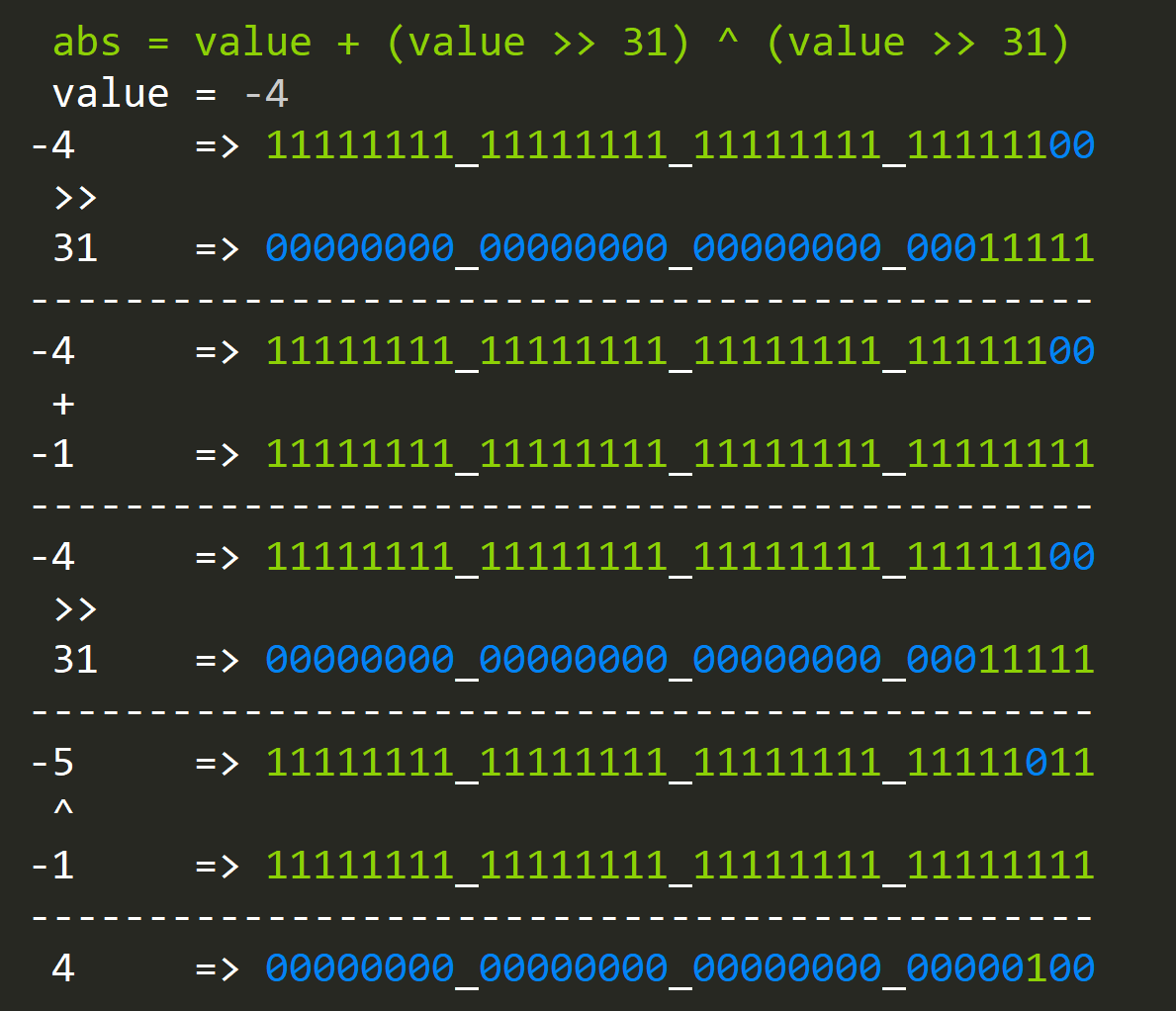
Since not all compilers are made equal a more portable version uses parenthesis to control order of operations:
abs = (value + (value >> 31)) ^ (value >> 31)
As you can see we check the sign first and if the value >= 0 the expression is trivial since it reduces to:
abs = (value + 0) ^ 0
If the number is less then zero things become more interesting:
abs = (value - 1)) ^ -1
but wait for a second, this looks exactly like the expression to negate the value:
negate = (value ^ -1) + 1
Indeed, to discover new bit hacks, you often need to start with simpler ones and use them in new expressions.
There are other ways to discover the more hardcore ones, but let's not get into this territory now.
Hardcore Bonus Content:
[Warning: Dragons be here!]
There's a really interesting bit hack that was discovered by multiple people for different purposes over the years, and it's very special since a lot of more complicated expressions depend on this one, especially when it comes to high-performance text handling.
- How to check if an Integer has any bytes that are zero?
Let's start with a simple method and let's check each byte by filling it all and then AND(ing) it with value and returning the result.
static bool hasZeroByte(int x)
{
if ((x & 0x000000FF) == 0)
return true;
if ((x & 0x0000FF00) == 0)
return true;
if ((x & 0x00FF0000) == 0)
return true;
if ((x & 0xFF000000) == 0)
return true;
return false;
}



That's a rather complicated algorithm, but fortunately for us, a better version was discovered that does all of this in a single expression.
static ulong hasZeroByte(ulong v)
{
return ((v) - 0x01010101UL) & ~(v) & 0x80808080UL;
}The explanation is not simple and requires a lot of effort and details, so I'm going to leave it for another time.
People that use it in more complex expressions don't really know how it works either.
Bit Hacks for Branch Elimination:
The important thing is that this expression opens doors to very interesting branch free algorithms that operate on strings.
So you might be wondering now, why go through all of this effort to discover bit hacks?
Performance, Performance, Performance. Sometimes bit hacks will be faster, but that's not always the case. Still, they play a critical role in performance even if it's indirect.
- We use them to write a branch-free code.
- We then use them to enable instruction-level parallelism without stalling.
Branch free code means that you don't need IF-Statements in your code.
But what's wrong with having branches?
[Note: This is a very simplified explanation, that contains just enough information to get the point across]
Nothing is wrong with them as long as they will be predicted correctly by the branch predictor. The Branch predictor is a hardware component that tries to predict which branch will be chosen next, and it's done to avoid jumps that could stall the instruction pipeline. The instructions will be scheduled ahead of time and executed. In a way, the branch predictor "learns" data access patterns and remembers the sequences to make a correct decision. Still, if our data access patterns are hard to guess or our data is very uniform, it's almost impossible.
So what happens if the "guess" that the Branch predictor made is incorrect? At some point, there will be a checkpoint, and the branch correctness will be checked, and if it's wrong, the whole pipeline will have to be thrown away, and it has to start again. It sounds (and is) expensive, so we would like to avoid branches in hot code paths if possible.
The issue is amplified when we're dealing with vectorization and SIMD Intrinsics code since we're interested in loading data into vectors as fast as we can to have performance benefits.
Let's look at a more concrete example of how to avoid branches in code:
public static int CountEven(int[] numbers)
{
int counter = 0;
for(int i = 0; i < numbers.Length; i++)
{
if(numbers[i] % 2 == 0)
{
counter++;
}
}
return counter;
}This simple function, given a set, will count how many even numbers are present in the set, if we run it on a reasonably big data set, we will get:
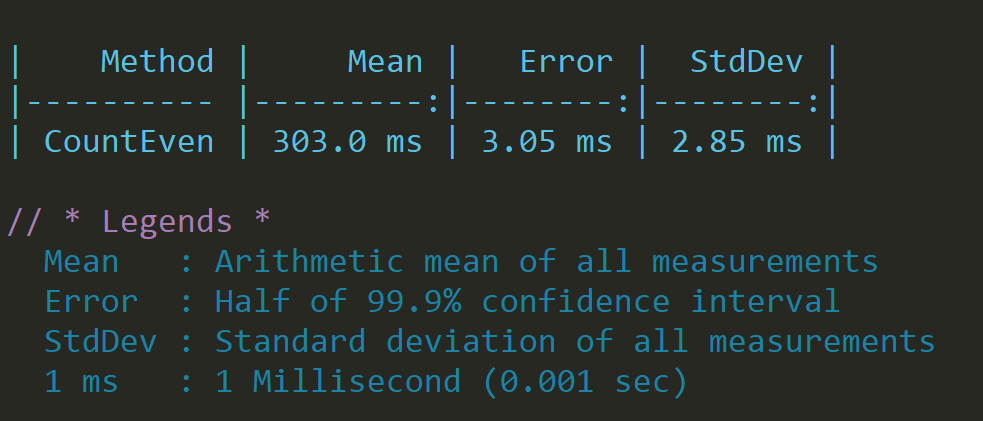
Not bad, but we can do better.
If you recall from previous examples, all odd numbers will have their first bit set to one, so to remove the branch, we have to AND it with one (1). This will return 1 when the number is odd and 0 if the number is even, but that's fine since we can count all odd numbers and subtract them from the set and get the desired result.
public static int CountEvenBranchFree(int[] numbers)
{
int counter = 0;
for (int i = 0; i < numbers.Length; i++)
{
var odd = numbers[i] & 1;
counter += odd;
}
// Take all odd numbers and substract them from the set
// leaving only even numbers
return numbers.Length - counter;
}What's the performance difference?

The branch free version is almost ten times faster.
Can we still do better (without resorting to SIMD)?
Sure we can; let's use instruction-level parallelism to break dependency chains between variables.
Uh Oh, what's that?
Processors try to execute as many instructions as possible; in fact, they can process multiple instructions simultaneously, on the same thread. The catch here is that the instructions cannot depend on each other.
[Note: Instruction-Level parallelism is beyond the scope of this article, and I'll expand upon it more in another article in the future]
So how do we break dependency chains? Having a single counter prevents us from executing multiple instructions at the same time, but if we create more than one and then combine them, we remove this limitation.
public static int CountEvenBranchFreeNoDeps(int[] numbers)
{
int c1 = 0;
int c2 = 0;
int c3 = 0;
int c4 = 0;
for (int i = 0; i < numbers.Length; i+=4)
{
var odd1 = numbers[i] & 1;
var odd2 = numbers[i + 1] & 1;
var odd3 = numbers[i + 2] & 1;
var odd4 = numbers[i + 3] & 1;
c1 += odd1;
c2 += odd2;
c3 += odd3;
c4 += odd4;
}
// Take all odd numbers and substract them from the set
// leaving only even numbers
return numbers.Length - c1 - c2 - c3 - c4;
}This change seems like a silly pseudo improvement but let's find out:
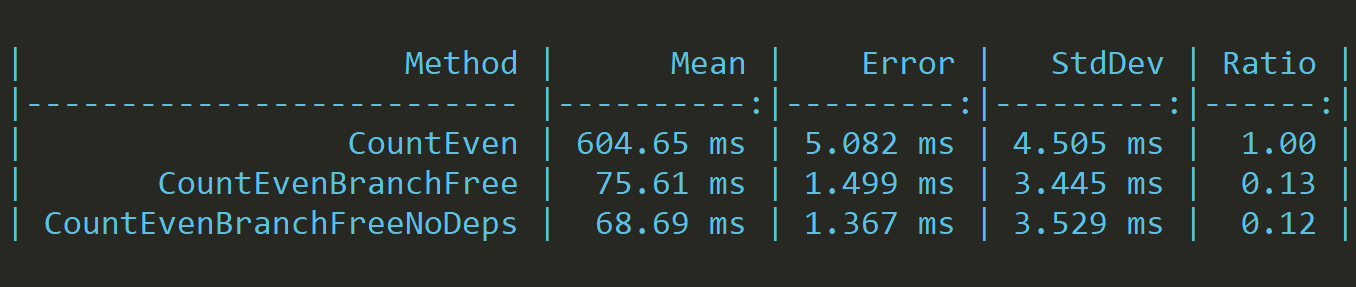
While not as impressive as the last result, we clearly see that there's small performance improvement.
Summary:
I hope that you see all of the benefits that bit hacks can bring to the table. This article shows only a few bit hacks and performance tricks that come with them, there's more.
Where to look for inspiration:
There are two videos that I've recorded to date that provide more information about bit hacks and even extend beyond the subject to SIMD and Instruction-Level parallelism:
- Fun with Bit Hacks in C#
- Instruction Level Dependency
There is also a video called "introduction to Bit Hacks" and uses mostly the same examples, but it's in a video form factor:
There are also very good books on the subject:
This is a free book about bit twiddling hacks, and it's absolutely phenomenal, and a must-read.
This is another awesome free book about floating-point operations, and again a must-read.
This a collection of programs to do low-level binary functions.
This content took a while to create, so if you like it, please consider buying me a coffee 😉



